Problema I
Dados los segmentos a y a·b, definir b, siendo la unidad el centímetro.Realizamos una división gráficamente:
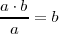
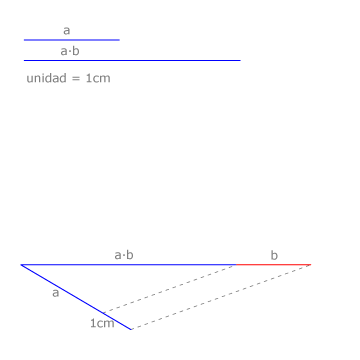
Dibujamos un haz de rectas. En una de ellas situamos a·b y en la otra a y la unidad, como se ve en la figura.
Trazamos la recta que une los extremos de a·b y de a y su paralela por el otro extremo del segmento unidad.
Obtenemos así b.
Problema II
Dados los segmentos a+b y a·b, definir a y b, siendo la unidad el centímetro.A partir del segmento producto calculamos la media proporcional de a y b, aplicando el teorema de la altura.
Aplicamos a continuación el teorema de la altura al segmento suma utilizando la media proporcional hallada.
Obtenemos las magnitudes a y b. Realmente hay dos soluciones pues cada segmento puede ser el menor o el mayor de los obtenidos.
Problema III
Dados los puntos alineados A,B y D Hallar el punto C que cumpla: (ABCD)=2/3.Dibujamos una recta a partir de B y situamos sobre ella los segmentos BX=2 y BY=3, considerando una unidad arbitraria.
Trazamos la recta CY y la paralela a BY desde A. Estas rectas se cortan en Z.
AZ=n. La recta XZ se corta con la recta dada en el punto C buscado.
Para comprobar:
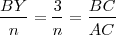, por otra parte,
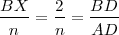, luego:
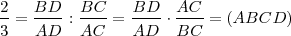
Problema IV
Dados los puntos alineados A,B y D Hallar el punto C que cumpla: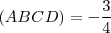
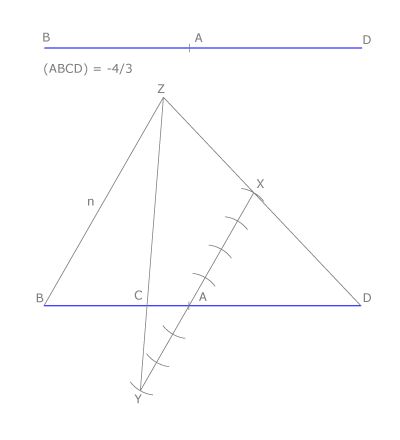
Dibujamos una recta a partir de A y situamos sobre ella los segmentos AX=4 y AY=3, considerando una unidad arbitraria y haciendo que AX y AY indiquen sentidos contrarios.
Trazamos la recta DX y la paralela a AX desde B. Estas rectas se cortan en Z.
BZ=n.
La recta YZ se corta con la recta dada en el punto C buscado.
Para comprobar:
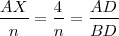, por otra parte,
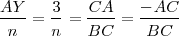, luego:
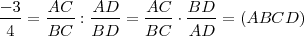
Problema V
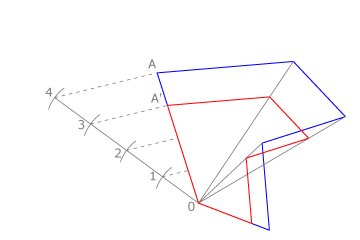
Dibujar una figura semejante a la dada cuyos lados estén en relación 3/4con los lados de la misma. Por uno de los vértices trazamos una recta en la que dibujamos cuatro unidades iguales y las numeramos.Trazamos la recta 4A y su paralela por el punto A'.
A' es el vértice de la figura semejante pues 0A’/0A = ¾.
Dibujamos diagonales de la figura dada y trazamos ordenadamente paralelas a sus lados, a partir de A'.
Problema VI
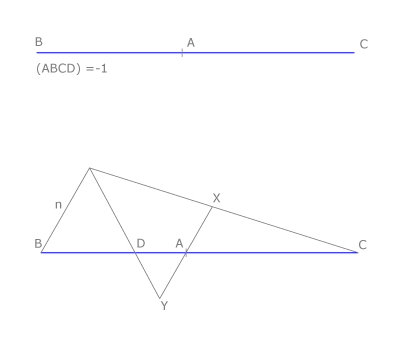
Dados los puntos alineados A,B y D Hallar el punto C que cumpla:(ABCD) = - 1
Trazamos por A una recta. Sobre ella situamos dos puntos X e Y, tal que AX = AY, teniendo en cuenta que los sentidos de AX y AY sean contrarios.
Dibujamos la recta CX y trazamos una paralela a AX por B. Estas rectas se cortan en Z.
BZ = n
Se cumple que:
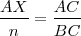
Por otra parte, la recta ZY corta a la recta dato en D.
Se cumple que:
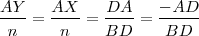, luego:
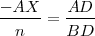
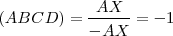
Problema VII
Dada la planta de una plaza circular de 30m de radio, situar una fuente hexagonal de lado AB=8m.Construimos la escala gráfica dividiendo en tres partes iguales el radio dado, hallando así el segmento que representa 10 metros reales.
Dibujamos la escala volante y dividimos una unidad en 10 partes iguales para poder medir en metros.
Dibujamos la fuente pedida.
