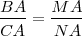Características generales
Consideramos que una variable x puede adquirir los valores a,b,c,d,... y otra variable los valores a' , b' , c' , d' , ... x e y son directamente proporcionales si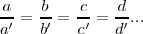
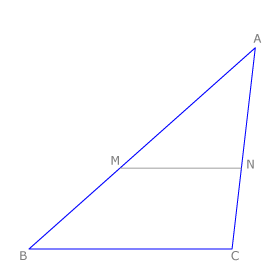
Teorema de Tales
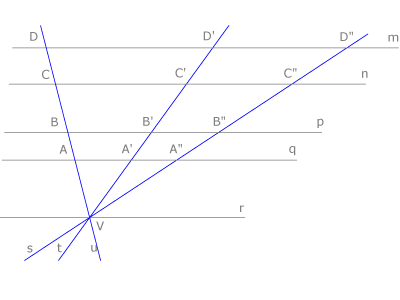
Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas: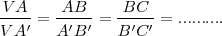
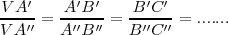
En Egipto, Tales de Mileto aplicó su teorema para medir la altura de una pirámide, considerando su sombra y situando un bastón
.
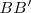En nuestra figura vemos que la altura
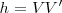es la incógnita de esta igualdad:
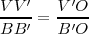, luego
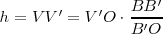
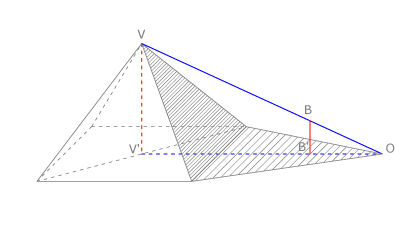
El teorema de Tales nos ofrece distintas expresiones de segmentos directamente proporcionales. Si nos fijamos en la figura tenemos que:
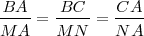
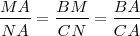
De la primera igualdad deducimos la segunda ya que:
